Time-series forecasting is an important research area that is critical to several scientific and industrial applications, like retail supply chain optimization, energy and traffic prediction, and weather forecasting. In retail use cases, for example, it has been observed that improving demand forecasting accuracy can meaningfully reduce inventory costs and increase revenue.
Modern time-series applications can involve forecasting hundreds of thousands of correlated time-series (e.g., demands of different products for a retailer) over long horizons (e.g., a quarter or year away at daily granularity). As such, time-series forecasting models need to satisfy the following key criterias:
- Ability to handle auxiliary features or covariates: Most use-cases can benefit tremendously from effectively using covariates, for instance, in retail forecasting, holidays and product specific attributes or promotions can affect demand.
- Suitable for different data modalities: It should be able to handle sparse count data, e.g., intermittent demand for a product with low volume of sales while also being able to model robust continuous seasonal patterns in traffic forecasting.
A number of neural network–based solutions have been able to show good performance on benchmarks and also support the above criterion. However, these methods are typically slow to train and can be expensive for inference, especially for longer horizons.
In “Long-term Forecasting with TiDE: Time-series Dense Encoder”, we present an all multilayer perceptron (MLP) encoder-decoder architecture for time-series forecasting that achieves superior performance on long horizon time-series forecasting benchmarks when compared to transformer-based solutions, while being 5–10x faster. Then in “On the benefits of maximum likelihood estimation for Regression and Forecasting”, we demonstrate that using a carefully designed training loss function based on maximum likelihood estimation (MLE) can be effective in handling different data modalities. These two works are complementary and can be applied as a part of the same model. In fact, they will be available soon in Google Cloud AI’s Vertex AutoML Forecasting.
TiDE: A simple MLP architecture for fast and accurate forecasting
Deep learning has shown promise in time-series forecasting, outperforming traditional statistical methods, especially for large multivariate datasets. After the success of transformers in natural language processing (NLP), there have been several works evaluating variants of the Transformer architecture for long horizon (the amount of time into the future) forecasting, such as FEDformer and PatchTST. However, other work has suggested that even linear models can outperform these transformer variants on time-series benchmarks. Nonetheless, simple linear models are not expressive enough to handle auxiliary features (e.g., holiday features and promotions for retail demand forecasting) and non-linear dependencies on the past.
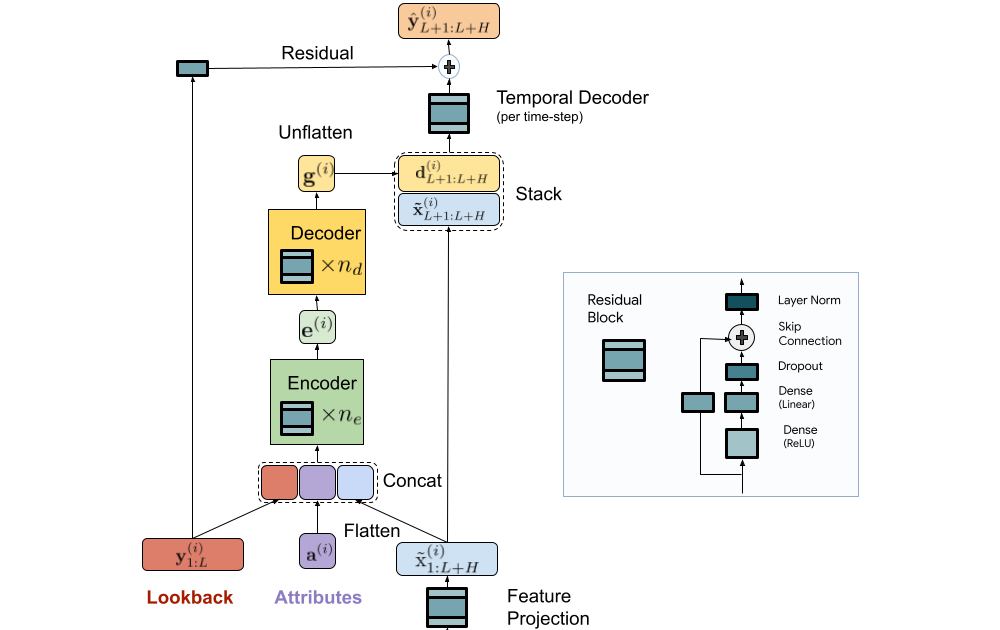
We present a scalable MLP-based encoder-decoder model for fast and accurate multi-step forecasting. Our model encodes the past of a time-series and all available features using an MLP encoder. Subsequently, the encoding is combined with future features using an MLP decoder to yield future predictions. The architecture is illustrated below.
 |
| TiDE model architecture for multi-step forecasting. |
TiDE is more than 10x faster in training compared to transformer-based baselines while being more accurate on benchmarks. Similar gains can be observed in inference as it only scales linearly with the length of the context (the number of time-steps the model looks back) and the prediction horizon. Below on the left, we show that our model can be 10.6% better than the best transformer-based baseline (PatchTST) on a popular traffic forecasting benchmark, in terms of test mean squared error (MSE). On the right, we show that at the same time our model can have much faster inference latency than PatchTST.
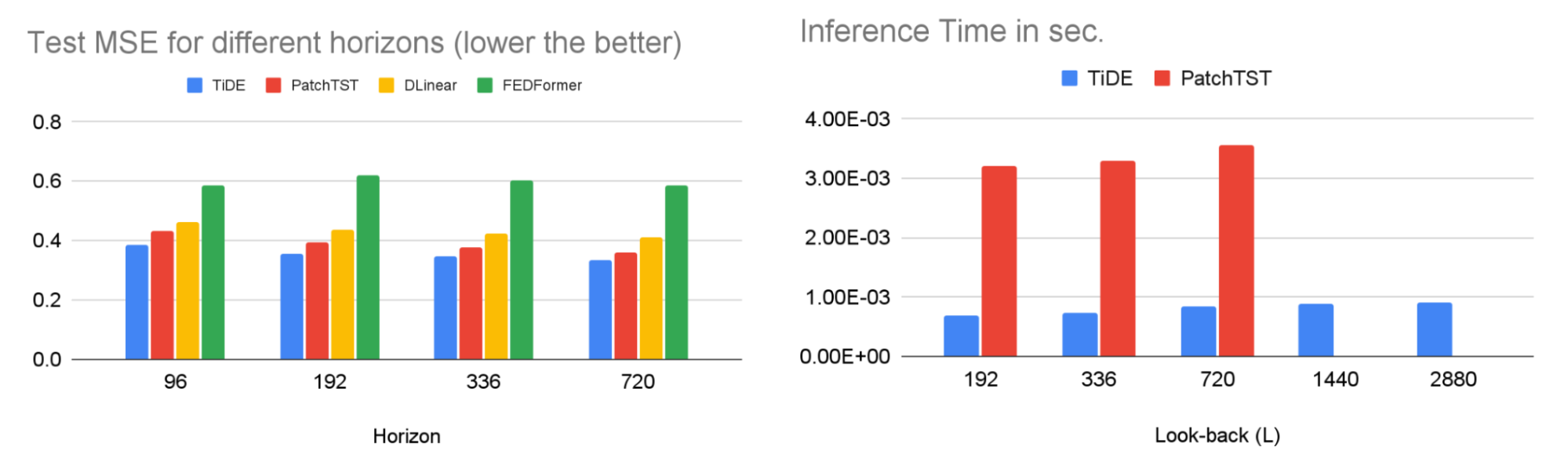 |
| Left: MSE on the test set of a popular traffic forecasting benchmark. Right: inference time of TiDE and PatchTST as a function of the look-back length. |
Our research demonstrates that we can take advantage of MLP’s linear computational scaling with look-back and horizon sizes without sacrificing accuracy, while transformers scale quadratically in this situation.
Probabilistic loss functions
In most forecasting applications the end user is interested in popular target metrics like the mean absolute percentage error (MAPE), weighted absolute percentage error (WAPE), etc. In such scenarios, the standard approach is to use the same target metric as the loss function while training. In “On the benefits of maximum likelihood estimation for Regression and Forecasting”, accepted at ICLR, we show that this approach might not always be the best. Instead, we advocate using the maximum likelihood loss for a carefully chosen family of distributions (discussed more below) that can capture inductive biases of the dataset during training. In other words, instead of directly outputting point predictions that minimize the target metric, the forecasting neural network predicts the parameters of a distribution in the chosen family that best explains the target data. At inference time, we can predict the statistic from the learned predictive distribution that minimizes the target metric of interest (e.g., the mean minimizes the MSE target metric while the median minimizes the WAPE). Further, we can also easily obtain uncertainty estimates of our forecasts, i.e., we can provide quantile forecasts by estimating the quantiles of the predictive distribution. In several use cases, accurate quantiles are vital, for instance, in demand forecasting a retailer might want to stock for the 90th percentile to guard against worst-case scenarios and avoid lost revenue.
The choice of the distribution family is crucial in such cases. For example, in the context of sparse count data, we might want to have a distribution family that can put more probability on zero, which is commonly known as zero-inflation. We propose a mixture of different distributions with learned mixture weights that can adapt to different data modalities. In the paper, we show that using a mixture of zero and multiple negative binomial distributions works well in a variety of settings as it can adapt to sparsity, multiple modalities, count data, and data with sub-exponential tails.
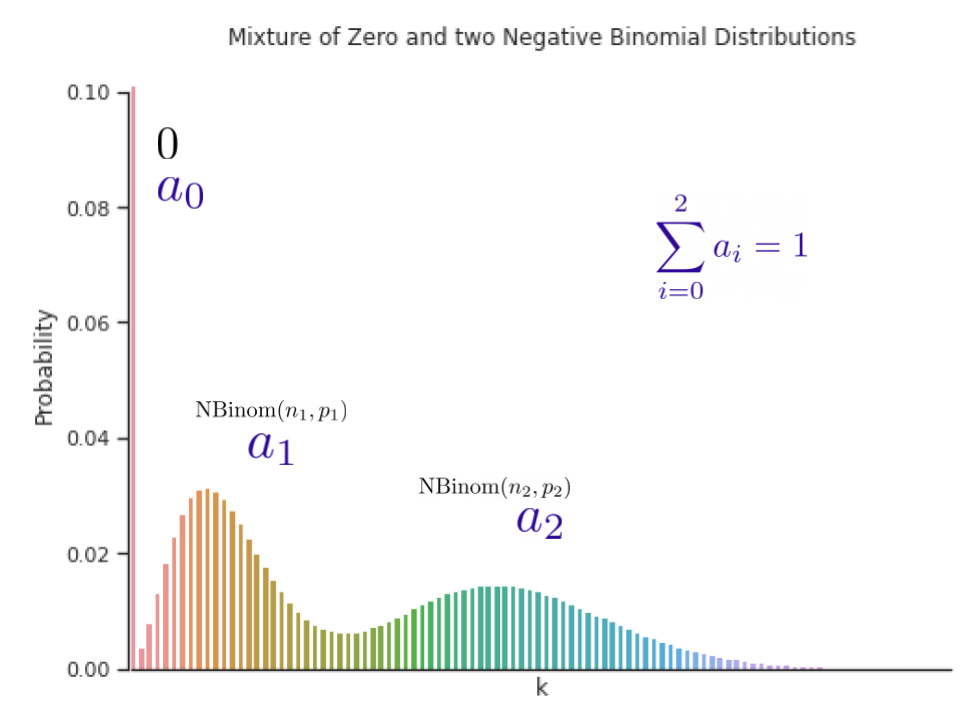 |
| A mixture of zero and two negative binomial distributions. The weights of the three components, a1, a2 and a3, can be learned during training. |
We use this loss function for training Vertex AutoML models on the M5 forecasting competition dataset and show that this simple change can lead to a 6% gain and outperform other benchmarks in the competition metric, weighted root mean squared scaled error (WRMSSE).
| M5 Forecasting | WRMSSE |
| Vertex AutoML | 0.639 +/- 0.007 |
| Vertex AutoML with probabilistic loss | 0.581 +/- 0.007 |
| DeepAR | 0.789 +/- 0.025 |
| FEDFormer | 0.804 +/- 0.033 |
Conclusion
We have shown how TiDE, together with probabilistic loss functions, enables fast and accurate forecasting that automatically adapts to different data distributions and modalities and also provides uncertainty estimates for its predictions. It provides state-of-the-art accuracy among neural network–based solutions at a fraction of the cost of previous transformer-based forecasting architectures, for large-scale enterprise forecasting applications. We hope this work will also spur interest in revisiting (both theoretically and empirically) MLP-based deep time-series forecasting models.
Acknowledgements
This work is the result of a collaboration between several individuals across Google Research and Google Cloud, including (in alphabetical order): Pranjal Awasthi, Dawei Jia, Weihao Kong, Andrew Leach, Shaan Mathur, Petros Mol, Shuxin Nie, Ananda Theertha Suresh, and Rose Yu.
Article Source link and Credit